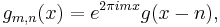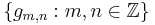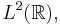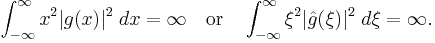Balian–Low theorem

In mathematics, the Balian–Low theorem in Fourier analysis is named for Roger Balian and Francis E. Low. The theorem states that no Gabor frame has a window function (or Gabor atom) g which is well-localized in both time and frequency.

Suppose g is a square-integrable function on the real line, and consider the so-called Gabor system

$g_{m,n}(x) = e^{2\pi i m x} g(x - n),$

for integers m and n. The Balian–Low theorem states that if

$\{g_{m,n}: m, n \in \mathbb{Z}\}$

is an orthonormal basis for the Hilbert space

$L^2(\mathbb{R}),$

then either

$\int_{-\infty}^\infty x^2 | g(x)|^2\; dx = \infty \quad \textrm{or} \quad \int_{-\infty}^\infty \xi^2|\hat{g}(\xi)|^2\; d\xi = \infty.$

The Balian–Low theorem has been extended to exact Gabor frames.

References

John J. Benedetto, Christopher Heil, and David F. Walnut (1994). "Differentiation and the Balian–Low Theorem". Journal of Fourier Analysis and Applications Volume 1, Number 4: 355–402. doi:10.1007/s00041-001-4016-5.

‹The stub template below has been proposed for renaming to . See stub types for deletion to help reach a consensus on what to do.
Feel free to edit the template, but the template must not be blanked, and this notice must not be removed, until the discussion is closed. For more information, read the guide to deletion.›

This article incorporates material from Balian-Low on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Balian–Low theorem

See also

References